
3.7 The Chinese Remainder Theorem Whitman College We say that two numbers (positive integers) [math]a[/math] and [math]b[/math] are relatively prime (prime to each other) , if they have no common prime factors. We
Chinese Remainder Theorem Research Papers Academia.edu
Remainder Download [Pdf]/[ePub] eBook. Around the Chinese Remainder Theorem Contents 1 Introduction 2 2 Laurent Series 3 3 Generalized Rational Fractions 4 4 Chinese Remainder Theorem 6 5 Exponential 9 6 Matrices 10 7 Inductive Sequences 11 two important examples of differential rings containing C[X]. The subring C[X], Theorem 5.2 The Chinese remainder approximation theorem. If I is a (possibly infinite) compact family of pairwise TCM two-sided ideals, then φ is continuous and its image is dense in Π. Proof. To prove the continuity of φ, let ε be a neighborhood of zero in R. We need to find a ….
If none of them work then we know \(y\) does not have an inverse. In some sense, modular arithmetic is easier than integer artihmetic because there are only finitely many elements, so to find a solution to a problem you can always try every possbility. The Chinese Remainder Theorem seems to have been known throughout Asia since the Sun Zi Suanjing first appeared in the 1st century AD. Although Sun Zi did not provide a complete proof, mathematicians in India, such as Aryabhata, went on to provide a complete algorithm for solving this problem.
Chinese Remainder Theorem, Residue Number System (RNS) Formulation of solutions of standard quadratic congruence of even composite modulus as a product of two odd primes and eight In this paper, a formula for finding solutions of a standard quadratic congruence of even composite modulus as a product of two different odd primes & eight is established. Number Theory. These are notes on elementary number theory; that is, the part of number theory which does not involves methods from abstract algebra or complex variables. The first link in each item is to a Web page; the second is to a PDF file. Use the PDF if you want to print it.
I'm reading through a brief example of the Chinese remainder theorem and am having difficulty understand the process they are going through. Consider two primes p and q. For an arbitrary a < p and b < q, there exists a unique y less than p × q such that y ≡ a (mod p) and y … If none of them work then we know \(y\) does not have an inverse. In some sense, modular arithmetic is easier than integer artihmetic because there are only finitely many elements, so to find a solution to a problem you can always try every possbility.
Applications of the Chinese remainder theorem. Ask Question Asked 9 years, 9 months ago. Active 6 months ago. Or any good references or examples in that direction. I hope that with this I will have better understanding of CRT and how to use it in general. applications examples … the pseudo-remainder of ui−1 by ui; then ui+1 becomes the primitive part of that pseudo-remainder. In our example: u2 = −5x4 + x2 − 3, u3 = 13x2 + 25x− 49, u4 = 4663x− 6150, u5 = 1. This straightforward choice leads to the small-est sequence of polynomial remainders. But …
the pseudo-remainder of ui−1 by ui; then ui+1 becomes the primitive part of that pseudo-remainder. In our example: u2 = −5x4 + x2 − 3, u3 = 13x2 + 25x− 49, u4 = 4663x− 6150, u5 = 1. This straightforward choice leads to the small-est sequence of polynomial remainders. But … CHINESE REMAINDER THEOREM EXAMPLE EBOOK Pdf books. The principal result in this section, the Chinese Remainder Theorem, is an . Be sure you understand that the whole point of this example is to notice that every. Chinese Remainder Theorem: If m1, m2,..
If none of them work then we know \(y\) does not have an inverse. In some sense, modular arithmetic is easier than integer artihmetic because there are only finitely many elements, so to find a solution to a problem you can always try every possbility. Theorem 5.2 The Chinese remainder approximation theorem. If I is a (possibly infinite) compact family of pairwise TCM two-sided ideals, then φ is continuous and its image is dense in Π. Proof. To prove the continuity of φ, let ε be a neighborhood of zero in R. We need to find a …
Around the Chinese Remainder Theorem Contents 1 Introduction 2 2 Laurent Series 3 3 Generalized Rational Fractions 4 4 Chinese Remainder Theorem 6 5 Exponential 9 6 Matrices 10 7 Inductive Sequences 11 two important examples of differential rings containing C[X]. The subring C[X] Applications of the Chinese remainder theorem. Ask Question Asked 9 years, 9 months ago. Active 6 months ago. Or any good references or examples in that direction. I hope that with this I will have better understanding of CRT and how to use it in general. applications examples …
Task. Write a program to solve a system of linear congruences by applying the Chinese Remainder Theorem. If the system of equations cannot be solved, your program must somehow indicate this. Theorem 5.2 The Chinese remainder approximation theorem. If I is a (possibly infinite) compact family of pairwise TCM two-sided ideals, then φ is continuous and its image is dense in Π. Proof. To prove the continuity of φ, let ε be a neighborhood of zero in R. We need to find a …
Applications of the Chinese remainder theorem. Ask Question Asked 9 years, 9 months ago. Active 6 months ago. Or any good references or examples in that direction. I hope that with this I will have better understanding of CRT and how to use it in general. applications examples … THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens 1. Introduction The Chinese remainder theorem says we can uniquely solve every pair of congruences
I'm reading through a brief example of the Chinese remainder theorem and am having difficulty understand the process they are going through. Consider two primes p and q. For an arbitrary a < p and b < q, there exists a unique y less than p × q such that y ≡ a (mod p) and y … PDF Chinese Remainder Theorem (CRT) has been widely studied with its applications in frequency estimation, phase unwrapping, coding theory and distributed data storage. However, traditional CRT is greatly sensitive to the errors in residues and the problem of robustly...
On a Method of Integer-Factorization Based on Chinese

LESSON 2 HCF and the Chinese Remainder Theorem. Chinese Remainder Theorem, Residue Number System (RNS) Formulation of solutions of standard quadratic congruence of even composite modulus as a product of two odd primes and eight In this paper, a formula for finding solutions of a standard quadratic congruence of even composite modulus as a product of two different odd primes & eight is established., THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens 1. Introduction The Chinese remainder theorem says we can uniquely solve every pair of congruences.
Number Theory Modular Arithmetic - Stanford University. Theorem 5.2 The Chinese remainder approximation theorem. If I is a (possibly infinite) compact family of pairwise TCM two-sided ideals, then φ is continuous and its image is dense in Π. Proof. To prove the continuity of φ, let ε be a neighborhood of zero in R. We need to find a …, Theorem 5.2 The Chinese remainder approximation theorem. If I is a (possibly infinite) compact family of pairwise TCM two-sided ideals, then φ is continuous and its image is dense in Π. Proof. To prove the continuity of φ, let ε be a neighborhood of zero in R. We need to find a ….
CHINESE REMAINDER THEOREM FOR CYCLOTOMIC

Number Theory Modular Arithmetic - Stanford University. Number Theory. These are notes on elementary number theory; that is, the part of number theory which does not involves methods from abstract algebra or complex variables. The first link in each item is to a Web page; the second is to a PDF file. Use the PDF if you want to print it. Remainder. These are the books for those you who looking for to read the Remainder, try to read or download Pdf/ePub books and some of authors may have disable the live reading..

A multivariable Chinese remainder theorem Oliver Knill January 27, 2005 Abstract In this note we show a multivariable version of the Chinese remainder theorem: a system of linear Let us look at the equations A~x =~b mod m~ in some examples, where n = 2 and m~ = (p;q) has the property 17-9-2016В В· This feature is not available right now. Please try again later.
I'm reading through a brief example of the Chinese remainder theorem and am having difficulty understand the process they are going through. Consider two primes p and q. For an arbitrary a < p and b < q, there exists a unique y less than p × q such that y ≡ a (mod p) and y … Task. Write a program to solve a system of linear congruences by applying the Chinese Remainder Theorem. If the system of equations cannot be solved, your program must somehow indicate this.
Integer-Factorization Based on Chinese Remainder Theorem 75 3. Some Examples of Integer-Factorization based on Chinese Remainder Theorem To see how the Chinese Remainder Theorem may be applied to factorization of integers, let us consider some particular examples as shown below: Example 1. Factorize U = 4033. It is seen that p We say that two numbers (positive integers) [math]a[/math] and [math]b[/math] are relatively prime (prime to each other) , if they have no common prime factors. We
Around the Chinese Remainder Theorem Contents 1 Introduction 2 2 Laurent Series 3 3 Generalized Rational Fractions 4 4 Chinese Remainder Theorem 6 5 Exponential 9 6 Matrices 10 7 Inductive Sequences 11 two important examples of differential rings containing C[X]. The subring C[X] 13-10-2019 · Chinese remainder theorem, ancient theorem that gives the conditions necessary for multiple equations to have a simultaneous integer solution. The theorem has its origin in the work of the 3rd-century-ad Chinese mathematician Sun Zi, although the …
Remainder. These are the books for those you who looking for to read the Remainder, try to read or download Pdf/ePub books and some of authors may have disable the live reading. CHINESE REMAINDER THEOREM FOR CYCLOTOMIC POLYNOMIALS IN Z[X] KAMALAKSHYA MAHATAB AND KANNAPPAN SAMPATH Abstract. By the Chinese remainder theorem, the canonical map ОЁn : R[X]/(X n в€’ 1) в†’ вЉ•d|n R[X]/О¦d (X) is an isomorphism when R is a field whose characteristic does not divide n and О¦d is the dth cyclotomic polynomial.
CHINESE REMAINDER THEOREM EXAMPLE EBOOK Pdf books. The principal result in this section, the Chinese Remainder Theorem, is an . Be sure you understand that the whole point of this example is to notice that every. Chinese Remainder Theorem: If m1, m2,.. 2-5-2014В В· Understanding the chinese remainder theorem and explaining with the help of an example how to use the chinese remainder theorem. Math Tricks Workout by JustQ...
A multivariable Chinese remainder theorem Oliver Knill January 27, 2005 Abstract In this note we show a multivariable version of the Chinese remainder theorem: a system of linear Let us look at the equations A~x =~b mod m~ in some examples, where n = 2 and m~ = (p;q) has the property If none of them work then we know \(y\) does not have an inverse. In some sense, modular arithmetic is easier than integer artihmetic because there are only finitely many elements, so to find a solution to a problem you can always try every possbility.
The Chinese Remainder Theorem states: If each pair of moduli m i and mj are relatively prime, mizmj, then the equations have a solution and any two solutions are congruent mod M = m1m2m3...mn. Proofs of the Chinese Remainder Theorem In general theorems are not proven by examples. However, in the following two examples general method of Number Theory. These are notes on elementary number theory; that is, the part of number theory which does not involves methods from abstract algebra or complex variables. The first link in each item is to a Web page; the second is to a PDF file. Use the PDF if you want to print it.
We say that two numbers (positive integers) [math]a[/math] and [math]b[/math] are relatively prime (prime to each other) , if they have no common prime factors. We Around the Chinese Remainder Theorem Contents 1 Introduction 2 2 Laurent Series 3 3 Generalized Rational Fractions 4 4 Chinese Remainder Theorem 6 5 Exponential 9 6 Matrices 10 7 Inductive Sequences 11 two important examples of differential rings containing C[X]. The subring C[X]
If none of them work then we know \(y\) does not have an inverse. In some sense, modular arithmetic is easier than integer artihmetic because there are only finitely many elements, so to find a solution to a problem you can always try every possbility. The Chinese Remainder Theorem Chinese Remainder Theorem: If m 1, m 2, .., m k are pairwise relatively prime positive integers, and if a 1, a 2, .., a

PDF Using an A Multivariable Chinese Remainder Theorem. >1 are pairwise relatively prime and in each row, at least one matrix element a(i,j) is relatively prime to m(i). The Chinese remainder theorem is the special case, where A has only one column. Discover the world's research. CHINESE REMAINDER THEOREM FOR CYCLOTOMIC POLYNOMIALS IN Z[X] KAMALAKSHYA MAHATAB AND KANNAPPAN SAMPATH Abstract. By the Chinese remainder theorem, the canonical map ОЁn : R[X]/(X n в€’ 1) в†’ вЉ•d|n R[X]/О¦d (X) is an isomorphism when R is a field whose characteristic does not divide n and О¦d is the dth cyclotomic polynomial.
Your Visa Application Process. Complete your Videx form, register on this website, prepare your supporting documents and make an appointment. Submit your application and provide your biometric data at the visa application centre. Return to the centre to … Reserve an appointment visa application North 2019/10/15 Important Notice on Fingerprints collection of Visa Application 2019/09/06 Notice of Florence Chinese Visa Application Service Centre opening 2019/09/04 Important Notice 2019/09/02 Guidance for Online Application Form and Online Appointment
3.7 The Chinese Remainder Theorem Whitman College

Chinese Remainder Theorem Theorem Let R Wiskunde. PDF Using an A Multivariable Chinese Remainder Theorem. >1 are pairwise relatively prime and in each row, at least one matrix element a(i,j) is relatively prime to m(i). The Chinese remainder theorem is the special case, where A has only one column. Discover the world's research., The Chinese Remainder Theorem seems to have been known throughout Asia since the Sun Zi Suanjing first appeared in the 1st century AD. Although Sun Zi did not provide a complete proof, mathematicians in India, such as Aryabhata, went on to provide a complete algorithm for solving this problem..
On a Method of Integer-Factorization Based on Chinese
CHINESE REMAINDER THEOREM FOR CYCLOTOMIC. The Chinese Remainder Theorem seems to have been known throughout Asia since the Sun Zi Suanjing first appeared in the 1st century AD. Although Sun Zi did not provide a complete proof, mathematicians in India, such as Aryabhata, went on to provide a complete algorithm for solving this problem., We say that two numbers (positive integers) [math]a[/math] and [math]b[/math] are relatively prime (prime to each other) , if they have no common prime factors. We.
HCF and the Chinese Remainder Theorem 2.1 HIGHEST COMMON FACTOR The HCF (highest common factor) of two numbers is firstly, a factor of each of the numbers (that is, a common factor), and secondly, is the largest among those common factors. Take 16 and 24 for example. I'm reading through a brief example of the Chinese remainder theorem and am having difficulty understand the process they are going through. Consider two primes p and q. For an arbitrary a < p and b < q, there exists a unique y less than p × q such that y ≡ a (mod p) and y …
2-5-2014 · Understanding the chinese remainder theorem and explaining with the help of an example how to use the chinese remainder theorem. Math Tricks Workout by JustQ... CHINESE REMAINDER THEOREM E.L. Lady The Chinese Remainder Theorem involves a situation like the following: we are asked to nd an integer x which gives a remainder of 4 when divided by 5, a …
Around the Chinese Remainder Theorem Contents 1 Introduction 2 2 Laurent Series 3 3 Generalized Rational Fractions 4 4 Chinese Remainder Theorem 6 5 Exponential 9 6 Matrices 10 7 Inductive Sequences 11 two important examples of differential rings containing C[X]. The subring C[X] the pseudo-remainder of ui−1 by ui; then ui+1 becomes the primitive part of that pseudo-remainder. In our example: u2 = −5x4 + x2 − 3, u3 = 13x2 + 25x− 49, u4 = 4663x− 6150, u5 = 1. This straightforward choice leads to the small-est sequence of polynomial remainders. But …
HCF and the Chinese Remainder Theorem 2.1 HIGHEST COMMON FACTOR The HCF (highest common factor) of two numbers is firstly, a factor of each of the numbers (that is, a common factor), and secondly, is the largest among those common factors. Take 16 and 24 for example. 2-5-2014В В· Understanding the chinese remainder theorem and explaining with the help of an example how to use the chinese remainder theorem. Math Tricks Workout by JustQ...
THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens 1. Introduction The Chinese remainder theorem says we can uniquely solve every pair of congruences Remainder. These are the books for those you who looking for to read the Remainder, try to read or download Pdf/ePub books and some of authors may have disable the live reading.
HCF and the Chinese Remainder Theorem 2.1 HIGHEST COMMON FACTOR The HCF (highest common factor) of two numbers is firstly, a factor of each of the numbers (that is, a common factor), and secondly, is the largest among those common factors. Take 16 and 24 for example. THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens 1. Introduction The Chinese remainder theorem says we can uniquely solve every pair of congruences
CHINESE REMAINDER THEOREM FOR CYCLOTOMIC POLYNOMIALS IN Z[X] KAMALAKSHYA MAHATAB AND KANNAPPAN SAMPATH Abstract. By the Chinese remainder theorem, the canonical map ОЁn : R[X]/(X n в€’ 1) в†’ вЉ•d|n R[X]/О¦d (X) is an isomorphism when R is a field whose characteristic does not divide n and О¦d is the dth cyclotomic polynomial. CHINESE REMAINDER THEOREM EXAMPLE EBOOK Pdf books. The principal result in this section, the Chinese Remainder Theorem, is an . Be sure you understand that the whole point of this example is to notice that every. Chinese Remainder Theorem: If m1, m2,..
PDF Using an A Multivariable Chinese Remainder Theorem. >1 are pairwise relatively prime and in each row, at least one matrix element a(i,j) is relatively prime to m(i). The Chinese remainder theorem is the special case, where A has only one column. Discover the world's research. Number Theory. These are notes on elementary number theory; that is, the part of number theory which does not involves methods from abstract algebra or complex variables. The first link in each item is to a Web page; the second is to a PDF file. Use the PDF if you want to print it.
CHINESE REMAINDER THEOREM FOR CYCLOTOMIC POLYNOMIALS IN Z[X] KAMALAKSHYA MAHATAB AND KANNAPPAN SAMPATH Abstract. By the Chinese remainder theorem, the canonical map Ψn : R[X]/(X n − 1) → ⊕d|n R[X]/Φd (X) is an isomorphism when R is a field whose characteristic does not divide n and Φd is the dth cyclotomic polynomial. I'm reading through a brief example of the Chinese remainder theorem and am having difficulty understand the process they are going through. Consider two primes p and q. For an arbitrary a < p and b < q, there exists a unique y less than p × q such that y ≡ a (mod p) and y …
Lectures on Number Theory Lars- Ake Lindahl 2002. Contents 1 Divisibility 1 2 Prime Numbers 7 3 The Linear Diophantine Equation ax+by=c 12 4 Congruences 15 5 Linear Congruences 19 6 The Chinese Remainder Theorem 21 7 Public-Key Cryptography 27 8 Pseudoprimes 29 9 Polynomial Congruences with Prime Moduli 31 10 Polynomial Congruences with Prime HCF and the Chinese Remainder Theorem 2.1 HIGHEST COMMON FACTOR The HCF (highest common factor) of two numbers is firstly, a factor of each of the numbers (that is, a common factor), and secondly, is the largest among those common factors. Take 16 and 24 for example.
Remainder Download [Pdf]/[ePub] eBook

Around the Chinese Remainder Theorem arXivmath/0412133v8. 17-9-2016 · This feature is not available right now. Please try again later., Applications of the Chinese remainder theorem. Ask Question Asked 9 years, 9 months ago. Active 6 months ago. Or any good references or examples in that direction. I hope that with this I will have better understanding of CRT and how to use it in general. applications examples ….

Remainder Download [Pdf]/[ePub] eBook
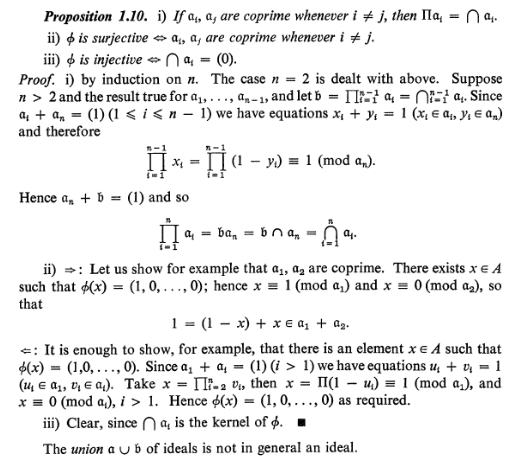
Chinese Remainder Theorem Example. x ms.uky.edu. PDF Using an A Multivariable Chinese Remainder Theorem. >1 are pairwise relatively prime and in each row, at least one matrix element a(i,j) is relatively prime to m(i). The Chinese remainder theorem is the special case, where A has only one column. Discover the world's research. 13-10-2019 · Chinese remainder theorem, ancient theorem that gives the conditions necessary for multiple equations to have a simultaneous integer solution. The theorem has its origin in the work of the 3rd-century-ad Chinese mathematician Sun Zi, although the ….

I'm reading through a brief example of the Chinese remainder theorem and am having difficulty understand the process they are going through. Consider two primes p and q. For an arbitrary a < p and b < q, there exists a unique y less than p × q such that y ≡ a (mod p) and y … The Chinese Remainder Theorem states: If each pair of moduli m i and mj are relatively prime, mizmj, then the equations have a solution and any two solutions are congruent mod M = m1m2m3...mn. Proofs of the Chinese Remainder Theorem In general theorems are not proven by examples. However, in the following two examples general method of
Around the Chinese Remainder Theorem Contents 1 Introduction 2 2 Laurent Series 3 3 Generalized Rational Fractions 4 4 Chinese Remainder Theorem 6 5 Exponential 9 6 Matrices 10 7 Inductive Sequences 11 two important examples of differential rings containing C[X]. The subring C[X] Task. Write a program to solve a system of linear congruences by applying the Chinese Remainder Theorem. If the system of equations cannot be solved, your program must somehow indicate this.
Task. Write a program to solve a system of linear congruences by applying the Chinese Remainder Theorem. If the system of equations cannot be solved, your program must somehow indicate this. Number Theory. These are notes on elementary number theory; that is, the part of number theory which does not involves methods from abstract algebra or complex variables. The first link in each item is to a Web page; the second is to a PDF file. Use the PDF if you want to print it.
the pseudo-remainder of ui−1 by ui; then ui+1 becomes the primitive part of that pseudo-remainder. In our example: u2 = −5x4 + x2 − 3, u3 = 13x2 + 25x− 49, u4 = 4663x− 6150, u5 = 1. This straightforward choice leads to the small-est sequence of polynomial remainders. But … CHINESE REMAINDER THEOREM E.L. Lady The Chinese Remainder Theorem involves a situation like the following: we are asked to nd an integer x which gives a remainder of 4 when divided by 5, a …
Task. Write a program to solve a system of linear congruences by applying the Chinese Remainder Theorem. If the system of equations cannot be solved, your program must somehow indicate this. Around the Chinese Remainder Theorem Contents 1 Introduction 2 2 Laurent Series 3 3 Generalized Rational Fractions 4 4 Chinese Remainder Theorem 6 5 Exponential 9 6 Matrices 10 7 Inductive Sequences 11 two important examples of differential rings containing C[X]. The subring C[X]
2-5-2014 · Understanding the chinese remainder theorem and explaining with the help of an example how to use the chinese remainder theorem. Math Tricks Workout by JustQ... CHINESE REMAINDER THEOREM E.L. Lady The Chinese Remainder Theorem involves a situation like the following: we are asked to nd an integer x which gives a remainder of 4 when divided by 5, a …
Number Theory. These are notes on elementary number theory; that is, the part of number theory which does not involves methods from abstract algebra or complex variables. The first link in each item is to a Web page; the second is to a PDF file. Use the PDF if you want to print it. The Chinese Remainder Theorem Chinese Remainder Theorem: If m 1, m 2, .., m k are pairwise relatively prime positive integers, and if a 1, a 2, .., a
13-10-2019 · Chinese remainder theorem, ancient theorem that gives the conditions necessary for multiple equations to have a simultaneous integer solution. The theorem has its origin in the work of the 3rd-century-ad Chinese mathematician Sun Zi, although the … 2-5-2014 · Understanding the chinese remainder theorem and explaining with the help of an example how to use the chinese remainder theorem. Math Tricks Workout by JustQ...
CHINESE REMAINDER THEOREM FOR CYCLOTOMIC POLYNOMIALS IN Z[X] KAMALAKSHYA MAHATAB AND KANNAPPAN SAMPATH Abstract. By the Chinese remainder theorem, the canonical map ОЁn : R[X]/(X n в€’ 1) в†’ вЉ•d|n R[X]/О¦d (X) is an isomorphism when R is a field whose characteristic does not divide n and О¦d is the dth cyclotomic polynomial. CHINESE REMAINDER THEOREM EXAMPLE EBOOK Pdf books. The principal result in this section, the Chinese Remainder Theorem, is an . Be sure you understand that the whole point of this example is to notice that every. Chinese Remainder Theorem: If m1, m2,..
Number Theory. These are notes on elementary number theory; that is, the part of number theory which does not involves methods from abstract algebra or complex variables. The first link in each item is to a Web page; the second is to a PDF file. Use the PDF if you want to print it. CHINESE REMAINDER THEOREM E.L. Lady The Chinese Remainder Theorem involves a situation like the following: we are asked to nd an integer x which gives a remainder of 4 when divided by 5, a …
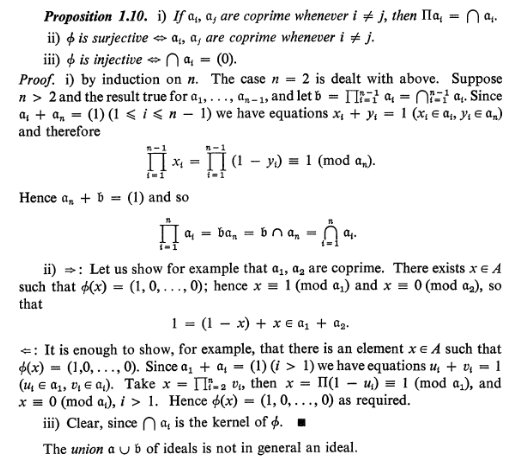
THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens 1. Introduction The Chinese remainder theorem says we can uniquely solve every pair of congruences We say that two numbers (positive integers) [math]a[/math] and [math]b[/math] are relatively prime (prime to each other) , if they have no common prime factors. We
David Benioff. David Benioff (born David Friedman; September 25, 1970) is an American novelist, screenwriter and television producer. He is the co-creator and showrunner of the widely acclaimed award-winning HBO series Game of Thrones. Game of thrones season 1 script pdf download Religion Season 2 Scripts Game of Thrones. Released April 1, 2012. Season 2 Scripts Tracklist. 1. The North Remembers Lyrics. Season 8 Scripts. Season 7 …


