Fonctions hyperboliques Site de Sébastien Pellerin L'égyptien Al-Hasib, surnommé « le Calculateur », a étudié les propriétés de la fonction tangente à la fin du IX e siècle. C'est pourquoi Al-Hasib a de lui-même défini la tangente comme étant l'outil idéal pour mesurer des hauteurs. En limitant l'application de la fonction tangente au triangle OAB rectangle en A, nous vérifions que
Fonction hyperbolique — Wikipédia
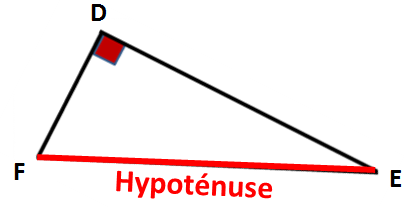
Application au triangle rectangle Site Web de Julien ÉLIE. On dit que les fonctions cosinus et sinus sont périodiques de période 2π. Conséquence : Pour tracer la courbe représentative de la fonction cosinus ou de la fonction sinus, il suffit de la tracer sur un intervalle de longueur 2π et de la compléter par translation. Méthode : Résoudre une équation trigonométrique, Exercice sur fonction Sinus, Cosinus : exercice de mathématiques de niveau terminale - Forum de mathématiques. Inscription gratuite . Etudier le signe de f'(x), en déduire le tableau de variation de la fonction , puis conclure. Merci de votre aide! Une photo de la figure est attaché.
II - La fonction sinus a. Définition La fonction qui à tout réel x, associe le réel sin(x) est appelée fonction sinus : sin : x→sin(x). b. Propriétés - Pour tout réel x, sin(−x)=−sin(x). On dit que la fonction sinus est une fonction impaire. Sa courbe représentative est donc symétrique par rapport à l’origine du repère. En analyse, la fonction sinus est une fonction de la variable réelle qui, à chaque réel α, associe le sinus de l'angle orienté de mesure α radians.C'est une fonction impaire et périodique.Les fonctions trigonométriques peuvent se définir ainsi géométriquement, mais les définitions plus modernes les caractérisent par des séries entières ou comme des solutions d'équations
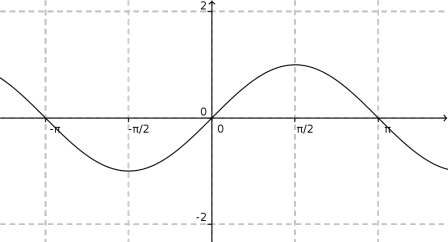
Utilisation du traceur de courbes en ligne. Le logiciel de tracé de courbes en ligne également appelé grapheur est un traceur de courbe en ligne qui permet de tracer des fonctions en ligne, il suffit de saisir l'expression en fonction de x de la fonction à tracer en utilisant les opérateurs mathématiques usuels. Le traceur de courbe est particulièrement adapté à l'étude de fonction On dit que la fonction sinus est 2π-périodique ou périodique de période 2π. Sa courbe représentative est donc invariante par translation de vecteur 2π ou −2π . - La fonction sinus est dérivable sur ℝ et ∀x∈ℝ , sin'(x)=cos(x) - Son tableau de variations :
Application: lim x→0 sin(2x) x =lim x→0 2 × sin(2x) 2x =2 Courbes représentatives • Les courbes de sin et cos sont des sinusoïdes. • On déduit la sinusoïde de cos par une translation de vecteur ~u =−π 2 ~ı de la sinusoïde de sin. −1 1 2π− π Période 2π ~u O cos x sin x PAUL MILAN DERNIÈRE IMPRESSION LE 17 novembre 2017 La fonction sinus est une fonction périodique de période 2, en effet pour tout réel x , sin(x + 2) = sin(x) La fonction sinus est antipériodique d'antipériode ; C'est aussi une fonction bornée, pour tout réel x on a : -1 sin(x) 1 ( voir sur le cercle trigonométrique ou avec quelques valeurs numériques) Variations de …
II - La fonction sinus a. Définition La fonction qui à tout réel x, associe le réel sin(x) est appelée fonction sinus : sin : x→sin(x). b. Propriétés - Pour tout réel x, sin(−x)=−sin(x). On dit que la fonction sinus est une fonction impaire. Sa courbe représentative est donc symétrique par rapport à l’origine du repère. 3.2 APPLICATION AUX CALCULS DE LIMITES Exemple : Déterminer la dérivée de la fonction suivante : f(x)=cos2x +cos2 x La fonction f est dérivable sur R car composée et produit de fonctions dérivables sur R f′(x)=−2sin2x −2sinxcosx =−2sin2x −sin2x =−3sin2x 3.2 Application aux calculs de limites Théorème 7 : D’après les fonctions dérivées des fonctions sinus et cosinus, on
Exercice sur fonction Sinus, Cosinus : exercice de mathématiques de niveau terminale - Forum de mathématiques. Inscription gratuite . Etudier le signe de f'(x), en déduire le tableau de variation de la fonction , puis conclure. Merci de votre aide! Une photo de la figure est attaché On définit la période T l’intervalle de temps au bout duquel la fonction se reproduit identiquement à elle-même; on dit alors que la fonction est périodique. Les fonctions sinus et cosinus sont définies à 2 près, soit 360° La période angulaire est donc Tang = 2 ou 360°
II - La fonction sinus a. Définition La fonction qui à tout réel x, associe le réel sin(x) est appelée fonction sinus : sin : x→sin(x). b. Propriétés - Pour tout réel x, sin(−x)=−sin(x). On dit que la fonction sinus est une fonction impaire. Sa courbe représentative est donc symétrique par rapport à l’origine du repère. On dit que la fonction sinus est 2π-périodique ou périodique de période 2π. Sa courbe représentative est donc invariante par translation de vecteur 2π ou −2π . - La fonction sinus est dérivable sur ℝ et ∀x∈ℝ , sin'(x)=cos(x) - Son tableau de variations :
Ce calcul est proposé dans un premier temps comme une application simple de la fonction sinus, supposée connue. Cette façon de procéder permet d’introduire la fonction cosinus en relation directe avec la fonction sinus, plus précisément le cosinus apparaît au travers de la relation cos(a)=sin(90°-a). On dit que la fonction sinus est 2π-périodique ou périodique de période 2π. Sa courbe représentative est donc invariante par translation de vecteur 2π ou −2π . - La fonction sinus est dérivable sur ℝ et ∀x∈ℝ , sin'(x)=cos(x) - Son tableau de variations :
Calcul de la fonction réciproque. Haut de page. Nous allons prendre un petit exemple pour voir comment calculer la fonction réciproque. Nous ne nous attarderons pas sur certaines hypothèses à vérifier (notamment les intervalles ou tout cela est vrai), ce n’est pas le but, nous allons voir principalement le … La fonction sinus est une fonction périodique de période 2, en effet pour tout réel x , sin(x + 2) = sin(x) La fonction sinus est antipériodique d'antipériode ; C'est aussi une fonction bornée, pour tout réel x on a : -1 sin(x) 1 ( voir sur le cercle trigonométrique ou avec quelques valeurs numériques) Variations de …
En analyse, la fonction sinus est une fonction de la variable réelle qui, à chaque réel α, associe le sinus de l'angle orienté de mesure α radians.C'est une fonction impaire et périodique.Les fonctions trigonométriques peuvent se définir ainsi géométriquement, mais les définitions plus modernes les caractérisent par des séries entières ou comme des solutions d'équations Exercice sur fonction Sinus, Cosinus : exercice de mathématiques de niveau terminale - Forum de mathématiques. Inscription gratuite . Etudier le signe de f'(x), en déduire le tableau de variation de la fonction , puis conclure. Merci de votre aide! Une photo de la figure est attaché
la dérivé de la fonction cosinus est l'inverse de la fonction sinus. Il a notamment: Cela peut être démontré par l'application d'une formule de Prosthaphaeresis pour calculer la limite de quotient cosinus:. la dérivée seconde fonction cosinus est identique avec le signe opposé: cependant, la fonction arc sinus prenant les mêmes valeurs, mais vue comme une application de [−,] dans , est injective mais pas surjective (par exemple, n'est l'image d'aucune valeur) donc pas bijective.
Fonctions cosinus et sinus maths sans échec
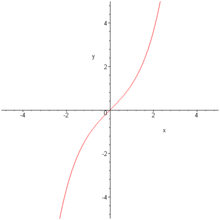
Cours sur les fonctions circulaires. Trouver la règle d'une fonction sinus Forme générale: f(x) = a sin b(x-h) + k Le paramètre h ne sera pas le même que celui de la fonction sinus. Par contre, le paramètre K est toujours le même que ce soit pour la fonction sinus que pour la fonction cosinus!, associés au point M sont les réels de la forme x0+2kπ où k est un entier relatif. Si M est un point du cercle trigonométrique, tout réel x associé à M par ce procédé est par définition une mesure en radian de l’angle orienté Š La ligne des sinus s’écrit :.
Fonctions sinus et cosinus.. Calcul de la fonction réciproque. Haut de page. Nous allons prendre un petit exemple pour voir comment calculer la fonction réciproque. Nous ne nous attarderons pas sur certaines hypothèses à vérifier (notamment les intervalles ou tout cela est vrai), ce n’est pas le but, nous allons voir principalement le …, cependant, la fonction arc sinus prenant les mêmes valeurs, mais vue comme une application de [−,] dans , est injective mais pas surjective (par exemple, n'est l'image d'aucune valeur) donc pas bijective..
Cosinus et Sinus cours de maths 2nde - cours de maths 1ère
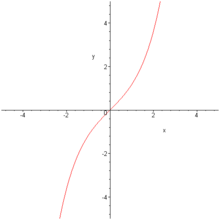
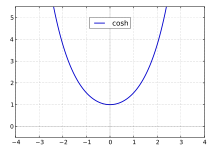
Chapitre 11. Fonctions sinus et cosinus. Le filtre sinus génère des textures basés sur des formes sinusoïdales, qui ressemblent à de l’eau, de la soie ou du bois contre-plaqué. Il fonctionne en utilisant deux couleurs différents définissables dans l’onglet couleurs. C’est deux couleurs génèrent ensuite des … La fonction cosinus hyperbolique est convexe.Elle intervient dans la définition de la chaînette, laquelle correspond à la forme que prend un câble suspendu à ses extrémités et soumis à son propre poids.. Puisque la fonction exponentielle peut être prolongée à l'ensemble des nombres complexes, nous pouvons aussi étendre les définitions des fonctions hyperboliques à l'ensemble des.

En analyse, la fonction sinus est une fonction de la variable réelle qui, à chaque réel α, associe le sinus de l'angle orienté de mesure α radians.C'est une fonction impaire et périodique.Les fonctions trigonométriques peuvent se définir ainsi géométriquement, mais les définitions plus modernes les caractérisent par des séries entières ou comme des solutions d'équations Application: lim x→0 sin(2x) x =lim x→0 2 × sin(2x) 2x =2 Courbes représentatives • Les courbes de sin et cos sont des sinusoïdes. • On déduit la sinusoïde de cos par une translation de vecteur ~u =−π 2 ~ı de la sinusoïde de sin. −1 1 2π− π Période 2π ~u O cos x sin x PAUL MILAN DERNIÈRE IMPRESSION LE 17 novembre 2017
3.2 APPLICATION AUX CALCULS DE LIMITES Exemple : Déterminer la dérivée de la fonction suivante : f(x)=cos2x +cos2 x La fonction f est dérivable sur R car composée et produit de fonctions dérivables sur R f′(x)=−2sin2x −2sinxcosx =−2sin2x −sin2x =−3sin2x 3.2 Application aux calculs de limites Théorème 7 : D’après les fonctions dérivées des fonctions sinus et cosinus, on Dec 01, 2009 · Fonction sinus, fonction cosinus Résumé du cours Fiches de révision de Mathématiques niveau Lycée regroupant les informations importantes sur les fonctions sinus et cosinus, à savoir : représentation graphique, parité, périodicité, dérivée, équivalence sur le cercle trigonométrique, etc.
I. Définition. La fonction cosinus est la fonction définie sur R par x → cos(x). La fonction sinus est la fonction définie sur R par x → sin(x). II. Propriété 1. Dérivabilité Rappel. Une fonction réelle (comme sinus ou cosinus) d’une variable x est dérivable en un point ou sur un intervalle réel ouvert non vide si elle est dérivable en chaque point de cet intervalle. 4°) Application à la dérivée de la composée d’une fonction affine suivie de la fonction sinus ou cosinus Rappel et b sont deux réels tels que a 0. u est une fonction définie et dérivable sur . est la fonction définie sur par f x u ax b .
II - La fonction sinus a. Définition La fonction qui à tout réel x, associe le réel sin(x) est appelée fonction sinus : sin : x→sin(x). b. Propriétés - Pour tout réel x, sin(−x)=−sin(x). On dit que la fonction sinus est une fonction impaire. Sa courbe représentative est donc symétrique par rapport à l’origine du repère. Académie de Nantes 3. Capacités et compétences Chercher, raisonner : mett e en œuv e les techniues vues en cou s concenant l’étude des fonctions. Modéliser : connaître les propriétés importantes de la fonction sinus cardinal, utiles pour le traitement du signal et
Dec 01, 2009 · Fonction sinus, fonction cosinus Résumé du cours Fiches de révision de Mathématiques niveau Lycée regroupant les informations importantes sur les fonctions sinus et cosinus, à savoir : représentation graphique, parité, périodicité, dérivée, équivalence sur le cercle trigonométrique, etc. Fonctions hyperboliques Cosinus et sinus hyperboliques. I Parité d'une fonction. Dénition 1 Une fonction f dénie sur R et à valeurs dans R est dite paire si et seulement si quelque soit x réel f (−x) = f (x) Une fonction f dénie sur R et à valeurs dans R est dite impaire si et seulement si quelque soit x réel f (−x) = −f (x) Exercice 1 Étudiez la parité des fonctions suivantes
Lorsque x parcourt [-π/2 ; π/2], la fonction sinus passe de la valeur -1 à la valeur 1. Elle est continue et dérivable, et ses tangentes sont horizontales aux extrémités de l'intervalle (les dérivées s'annulent en -π/2 et π/2). Cela en fait donc une fonction de choix pour remplacer une fonction de … |\bullet| Si le paramètreh| est positif, le graphique de la fonction sinus se déplacera vers la droite.\bullet| Si le paramètreh| est négatif, le graphique de la fonction sinus se déplacera vers la gauche. Analyse du paramètrek| Le paramètrek| est responsable de l'ordonnée moyenne (l'axe d'oscillation) du graphique de la
|\bullet| Si le paramètreh| est positif, le graphique de la fonction sinus se déplacera vers la droite.\bullet| Si le paramètreh| est négatif, le graphique de la fonction sinus se déplacera vers la gauche. Analyse du paramètrek| Le paramètrek| est responsable de l'ordonnée moyenne (l'axe d'oscillation) du graphique de la Nous vous rappelons que les notions et outils de base relatifs aux études des Fonctions sinus et cosinus constituent une part importante de la culture générale dont vous devez disposer en
Oct 13, 2013 · Application de la formule : sin(p) + sin(q) Démonstration de la formule d'addition pour la fonction sinus limite de fonction avec cosinus et sinus • théorème des gendarmes 4°) Application à la dérivée de la composée d’une fonction affine suivie de la fonction sinus ou cosinus Rappel et b sont deux réels tels que a 0. u est une fonction définie et dérivable sur . est la fonction définie sur par f x u ax b .
Apr 13, 2014 · Présentation de la fonction sinus à partir de la projection du mouvement circulaire. Sur http://www.clipedia.be, vous trouverez d'autres vidéos courtes et am... Ce calcul est proposé dans un premier temps comme une application simple de la fonction sinus, supposée connue. Cette façon de procéder permet d’introduire la fonction cosinus en relation directe avec la fonction sinus, plus précisément le cosinus apparaît au travers de la relation cos(a)=sin(90°-a).
L'égyptien Al-Hasib, surnommé « le Calculateur », a étudié les propriétés de la fonction tangente à la fin du IX e siècle. C'est pourquoi Al-Hasib a de lui-même défini la tangente comme étant l'outil idéal pour mesurer des hauteurs. En limitant l'application de la fonction tangente au triangle OAB rectangle en A, nous vérifions que Le filtre sinus génère des textures basés sur des formes sinusoïdales, qui ressemblent à de l’eau, de la soie ou du bois contre-plaqué. Il fonctionne en utilisant deux couleurs différents définissables dans l’onglet couleurs. C’est deux couleurs génèrent ensuite des …
En analyse, la fonction sinus est une fonction de la variable réelle qui, à chaque réel α, associe le sinus de l'angle orienté de mesure α radians.C'est une fonction impaire et périodique.Les fonctions trigonométriques peuvent se définir ainsi géométriquement, mais les définitions plus modernes les caractérisent par des séries entières ou comme des solutions d'équations Utilisation du traceur de courbes en ligne. Le logiciel de tracé de courbes en ligne également appelé grapheur est un traceur de courbe en ligne qui permet de tracer des fonctions en ligne, il suffit de saisir l'expression en fonction de x de la fonction à tracer en utilisant les opérateurs mathématiques usuels. Le traceur de courbe est particulièrement adapté à l'étude de fonction
Analysons la fonction sinus en générale Prenons f(x) = sin x
Cours Fonctions sinus et cosinus – Mathématiques – BAC S. Application fonction cosinus - Forum de mathématiques. Inscription gratuite . La continuité de la fonction f est importante à préciser, le fait que [0,2pi] soit un compact aussi et c'est ensuite après que tu dois faire des calculs pour déterminer exactement l'intervalle image., Exercice sur fonction Sinus, Cosinus : exercice de mathématiques de niveau terminale - Forum de mathématiques. Inscription gratuite . Etudier le signe de f'(x), en déduire le tableau de variation de la fonction , puis conclure. Merci de votre aide! Une photo de la figure est attaché.
Fonctions cosinus et sinus maths sans échec
Fonctions sinus et cosinus les exercices. La fonction cosinus hyperbolique est convexe.Elle intervient dans la définition de la chaînette, laquelle correspond à la forme que prend un câble suspendu à ses extrémités et soumis à son propre poids.. Puisque la fonction exponentielle peut être prolongée à l'ensemble des nombres complexes, nous pouvons aussi étendre les définitions des fonctions hyperboliques à l'ensemble des, Académie de Nantes 3. Capacités et compétences Chercher, raisonner : mett e en œuv e les techniues vues en cou s concenant l’étude des fonctions. Modéliser : connaître les propriétés importantes de la fonction sinus cardinal, utiles pour le traitement du signal et.
b < 0 f(x) = sin (-x) est le graphique de couleur bleu Le point (h,k) détermine le point de départ du cycle pour la fonction sinus. Si ab > 0, la courbe est croissante, les paramètres « a » et « b » seront positifs ou ils seront tous les deux négatifs. De façon générale, on met les deux paramètres positifs. B.1 Reciproque de la fonction sinus hyperbolique´ I La fonction sh est continue et strictement croissante sur R, elle r´ealise donc une bijection de cet intervalle sur son image R et on peut d´efinir son application r´eciproque. B.1.1 D´efinition On appelle fonction argument sinus hyperbolique, et on note Argsh : …
La fonction \(x\longmapsto \cos x\) est une fonction paire. Complément : Démonstration Il suffit de se rappeler les propriétés fondamentales de Sinus et Cosinus : En analyse, la fonction sinus est une fonction de la variable réelle qui, à chaque réel α, associe le sinus de l'angle orienté de mesure α radians.C'est une fonction impaire et périodique.Les fonctions trigonométriques peuvent se définir ainsi géométriquement, mais les définitions plus modernes les caractérisent par des séries entières ou comme des solutions d'équations
La courbe représentative de la fonction sinusLes points d'intersection des courbes des fonctions sinus et cosinus . Angles associés. Apprendre. Angles associés Démonstration de la formule sin² x + cos² x = 1 Exemple d'application de la formule sin² x + cos² x = 1 Savoir et savoir-faire. S'entraîner . … associés au point M sont les réels de la forme x0+2kπ où k est un entier relatif. Si M est un point du cercle trigonométrique, tout réel x associé à M par ce procédé est par définition une mesure en radian de l’angle orienté Š La ligne des sinus s’écrit :
Trouver la règle d'une fonction sinus Forme générale: f(x) = a sin b(x-h) + k Le paramètre h ne sera pas le même que celui de la fonction sinus. Par contre, le paramètre K est toujours le même que ce soit pour la fonction sinus que pour la fonction cosinus! Plus précisément, en théorie de l'information, la fonction sinus cardinal permet la synthèse exacte des signaux à spectre de support fini (formule de Shannon, 1949). En particulier, le sinus cardinal est fréquemment rencontré en théorie des antennes, en acoustique, en radar, pour la …
Académie de Nantes 3. Capacités et compétences Chercher, raisonner : mett e en œuv e les techniues vues en cou s concenant l’étude des fonctions. Modéliser : connaître les propriétés importantes de la fonction sinus cardinal, utiles pour le traitement du signal et L'égyptien Al-Hasib, surnommé « le Calculateur », a étudié les propriétés de la fonction tangente à la fin du IX e siècle. C'est pourquoi Al-Hasib a de lui-même défini la tangente comme étant l'outil idéal pour mesurer des hauteurs. En limitant l'application de la fonction tangente au triangle OAB rectangle en A, nous vérifions que
Application de la linéarisation trigonométrique. La linéarisation trigonométrique peut s'avérer très utile pour le calcul de primitive faisant intervenir des puissances de sinus ou de cosinus. L'arc sinus est la fonction réciproque de la fonction sinus. Arc tangente: arctan. La fonction arctan permet le calcul de … Nous vous rappelons que les notions et outils de base relatifs aux études des Fonctions sinus et cosinus constituent une part importante de la culture générale dont vous devez disposer en
La fonction cosinus, notée cos, est la fonction qui à tout réel x associe le nombre réel cosx. La fonction sinus, notée sin, est la fonction qui à tout réel x associe le nombre réel sinx. Propriétés : les fonctions sinus et cosinus sont dérivables sur l'ensemble des réels. 4°) Application à la dérivée de la composée d’une fonction affine suivie de la fonction sinus ou cosinus Rappel et b sont deux réels tels que a 0. u est une fonction définie et dérivable sur . est la fonction définie sur par f x u ax b .
associés au point M sont les réels de la forme x0+2kπ où k est un entier relatif. Si M est un point du cercle trigonométrique, tout réel x associé à M par ce procédé est par définition une mesure en radian de l’angle orienté Š La ligne des sinus s’écrit : Dec 01, 2009 · Fonction sinus, fonction cosinus Résumé du cours Fiches de révision de Mathématiques niveau Lycée regroupant les informations importantes sur les fonctions sinus et cosinus, à savoir : représentation graphique, parité, périodicité, dérivée, équivalence sur le cercle trigonométrique, etc.
cependant, la fonction arc sinus prenant les mêmes valeurs, mais vue comme une application de [−,] dans , est injective mais pas surjective (par exemple, n'est l'image d'aucune valeur) donc pas bijective. cependant, la fonction arc sinus prenant les mêmes valeurs, mais vue comme une application de [−,] dans , est injective mais pas surjective (par exemple, n'est l'image d'aucune valeur) donc pas bijective.
Dec 01, 2009 · Fonction sinus, fonction cosinus Résumé du cours Fiches de révision de Mathématiques niveau Lycée regroupant les informations importantes sur les fonctions sinus et cosinus, à savoir : représentation graphique, parité, périodicité, dérivée, équivalence sur le cercle trigonométrique, etc. B.1 Reciproque de la fonction sinus hyperbolique´ I La fonction sh est continue et strictement croissante sur R, elle r´ealise donc une bijection de cet intervalle sur son image R et on peut d´efinir son application r´eciproque. B.1.1 D´efinition On appelle fonction argument sinus hyperbolique, et on note Argsh : …
Trouver la règle d'une fonction sinus Forme générale: f(x) = a sin b(x-h) + k Le paramètre h ne sera pas le même que celui de la fonction sinus. Par contre, le paramètre K est toujours le même que ce soit pour la fonction sinus que pour la fonction cosinus! Nov 09, 2013 · Fonction sinus [Résolu] - Algorithmes / Méthodes Articles Tinder fonctionnement - Articles Snapchat vous a ajouté depuis la fonction - Conseils pratiques - Messagerie instantanée . 12 réponses. Hello ! Travaillant sur une application de maths, je suis bien tenté de réécrire ma propre version de la fonction sinus, mais je ne sais pas
La fonction sinus YouTube

Les modifications des paramètres dans une fonction sinus. Dec 01, 2009 · Fonction sinus, fonction cosinus Résumé du cours Fiches de révision de Mathématiques niveau Lycée regroupant les informations importantes sur les fonctions sinus et cosinus, à savoir : représentation graphique, parité, périodicité, dérivée, équivalence sur le cercle trigonométrique, etc., Calcul de la fonction réciproque. Haut de page. Nous allons prendre un petit exemple pour voir comment calculer la fonction réciproque. Nous ne nous attarderons pas sur certaines hypothèses à vérifier (notamment les intervalles ou tout cela est vrai), ce n’est pas le but, nous allons voir principalement le ….
Fonctions sinus et cosinus les exercices

Cosinus et Sinus cours de maths 2nde - cours de maths 1ère. II - La fonction sinus a. Définition La fonction qui à tout réel x, associe le réel sin(x) est appelée fonction sinus : sin : x→sin(x). b. Propriétés - Pour tout réel x, sin(−x)=−sin(x). On dit que la fonction sinus est une fonction impaire. Sa courbe représentative est donc symétrique par rapport à l’origine du repère. Utilisation du traceur de courbes en ligne. Le logiciel de tracé de courbes en ligne également appelé grapheur est un traceur de courbe en ligne qui permet de tracer des fonctions en ligne, il suffit de saisir l'expression en fonction de x de la fonction à tracer en utilisant les opérateurs mathématiques usuels. Le traceur de courbe est particulièrement adapté à l'étude de fonction.
En connaissant le Cosinus ( Cos) de l’angle, la fonction réciproque Arccosinus ( Arccos ), permet de trouver la mesure de l’angle. En utilisant la calculatrice, il faut la mettre en degré “deg” et tu utilises la fonction réciproque Arccosinus ( ou cos-1 ) pour avoir la mesure de l’angle. Exercice d’application : … On dit que la fonction sinus est 2π-périodique ou périodique de période 2π. Sa courbe représentative est donc invariante par translation de vecteur 2π ou −2π . - La fonction sinus est dérivable sur ℝ et ∀x∈ℝ , sin'(x)=cos(x) - Son tableau de variations :
Nous vous rappelons que les notions et outils de base relatifs aux études des Fonctions sinus et cosinus constituent une part importante de la culture générale dont vous devez disposer en I. Définition. La fonction cosinus est la fonction définie sur R par x → cos(x). La fonction sinus est la fonction définie sur R par x → sin(x). II. Propriété 1. Dérivabilité Rappel. Une fonction réelle (comme sinus ou cosinus) d’une variable x est dérivable en un point ou sur un intervalle réel ouvert non vide si elle est dérivable en chaque point de cet intervalle.
Sinus et cosinus dans le cercle trigonométrique Dans le cercle trigonométrique le cosinus d'un angle "α" correspond à l'abscisse du point repéré par cet angle tandis que le sinus correspond à l'ordonnée de ce point.En effet, le centre O du cercle, le point M associé à l'angle α et la projection de M sur sur l'axe des abscisse (que l'on peut noter M x) constituent un triangle: Sinus et cosinus dans le cercle trigonométrique Dans le cercle trigonométrique le cosinus d'un angle "α" correspond à l'abscisse du point repéré par cet angle tandis que le sinus correspond à l'ordonnée de ce point.En effet, le centre O du cercle, le point M associé à l'angle α et la projection de M sur sur l'axe des abscisse (que l'on peut noter M x) constituent un triangle:
La fonctionest une fonction définie et continue sur par composition de la fonction sinus par la fonction valeur absolue, toutes deux continues sur . Exercice corrigé 4 (2 questions) Niveau : facile Correction de l’exercice 4 Retour au menu 4°) Application à la dérivée de la composée d’une fonction affine suivie de la fonction sinus ou cosinus Rappel et b sont deux réels tels que a 0. u est une fonction définie et dérivable sur . est la fonction définie sur par f x u ax b .
En analyse, la fonction sinus est une fonction de la variable réelle qui, à chaque réel α, associe le sinus de l'angle orienté de mesure α radians.C'est une fonction impaire et périodique.Les fonctions trigonométriques peuvent se définir ainsi géométriquement, mais les définitions plus modernes les caractérisent par des séries entières ou comme des solutions d'équations b < 0 f(x) = sin (-x) est le graphique de couleur bleu Le point (h,k) détermine le point de départ du cycle pour la fonction sinus. Si ab > 0, la courbe est croissante, les paramètres « a » et « b » seront positifs ou ils seront tous les deux négatifs. De façon générale, on met les deux paramètres positifs.
Nous vous rappelons que les notions et outils de base relatifs aux études des Fonctions sinus et cosinus constituent une part importante de la culture générale dont vous devez disposer en Ce calcul est proposé dans un premier temps comme une application simple de la fonction sinus, supposée connue. Cette façon de procéder permet d’introduire la fonction cosinus en relation directe avec la fonction sinus, plus précisément le cosinus apparaît au travers de la relation cos(a)=sin(90°-a).
Nov 09, 2013 · Fonction sinus [Résolu] - Algorithmes / Méthodes Articles Tinder fonctionnement - Articles Snapchat vous a ajouté depuis la fonction - Conseils pratiques - Messagerie instantanée . 12 réponses. Hello ! Travaillant sur une application de maths, je suis bien tenté de réécrire ma propre version de la fonction sinus, mais je ne sais pas Calcul de la fonction réciproque. Haut de page. Nous allons prendre un petit exemple pour voir comment calculer la fonction réciproque. Nous ne nous attarderons pas sur certaines hypothèses à vérifier (notamment les intervalles ou tout cela est vrai), ce n’est pas le but, nous allons voir principalement le …
Apr 13, 2014 · Présentation de la fonction sinus à partir de la projection du mouvement circulaire. Sur http://www.clipedia.be, vous trouverez d'autres vidéos courtes et am... La fonction sinus est une fonction périodique de période 2, en effet pour tout réel x , sin(x + 2) = sin(x) La fonction sinus est antipériodique d'antipériode ; C'est aussi une fonction bornée, pour tout réel x on a : -1 sin(x) 1 ( voir sur le cercle trigonométrique ou avec quelques valeurs numériques) Variations de …
Application: lim x→0 sin(2x) x =lim x→0 2 × sin(2x) 2x =2 Courbes représentatives • Les courbes de sin et cos sont des sinusoïdes. • On déduit la sinusoïde de cos par une translation de vecteur ~u =−π 2 ~ı de la sinusoïde de sin. −1 1 2π− π Période 2π ~u O cos x sin x PAUL MILAN DERNIÈRE IMPRESSION LE 17 novembre 2017 Application fonction cosinus - Forum de mathématiques. Inscription gratuite . La continuité de la fonction f est importante à préciser, le fait que [0,2pi] soit un compact aussi et c'est ensuite après que tu dois faire des calculs pour déterminer exactement l'intervalle image.
B.1 Reciproque de la fonction sinus hyperbolique´ I La fonction sh est continue et strictement croissante sur R, elle r´ealise donc une bijection de cet intervalle sur son image R et on peut d´efinir son application … Académie de Nantes 3. Capacités et compétences Chercher, raisonner : mett e en œuv e les techniues vues en cou s concenant l’étude des fonctions. Modéliser : connaître les propriétés importantes de la fonction sinus cardinal, utiles pour le traitement du signal et
La fonction cosinus hyperbolique est convexe.Elle intervient dans la définition de la chaînette, laquelle correspond à la forme que prend un câble suspendu à ses extrémités et soumis à son propre poids.. Puisque la fonction exponentielle peut être prolongée à l'ensemble des nombres complexes, nous pouvons aussi étendre les définitions des fonctions hyperboliques à l'ensemble des La fonction cosinus hyperbolique est convexe.Elle intervient dans la définition de la chaînette, laquelle correspond à la forme que prend un câble suspendu à ses extrémités et soumis à son propre poids.. Puisque la fonction exponentielle peut être prolongée à l'ensemble des nombres complexes, nous pouvons aussi étendre les définitions des fonctions hyperboliques à l'ensemble des